An Array can be defined as a Linear arrangement, which may be a collection of knowledge items having similar data types and stored in contiguous memory locations. By knowing the address of the primary item we will easily access all items/elements of an array. So, lets delve into the topic, Types of Arrays with examples galore.
Introduction
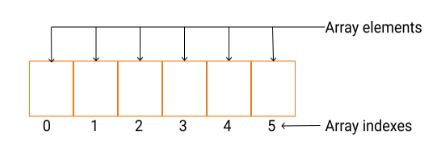
Array Index: It signifies the position of an element in an array. It always start with 0.
Elements in an array: The items in an array. These are access by their index.
Length of an array: The total number of elements in an array equals the length of an array.
Note : Whenever we declare and create an array, the compiler allocates enough memory to carry all elements of knowledge .
For example, an array declared with value [5] as in int A[5] will have 5 elements with index ranging from 0 to 4 and therefore the memory allocated contiguously are going to be 10 bytes. The compiler knows the address of the primary byte of the array only. Also, the address of the primary byte is take into account because the memory address for the entire array.
The concept of arrays came when we needed to perform the same operations on a number of variables. So performing the same operation over and over again seem tedious and therefore, the concept of arrays was introduce. Due to arrays only a single variable can store ‘n’ values, which would have been traditionally stored in ‘n’ variables.
Significance of the Index starting at 0
Let’s attempt to understand this by taking one example. Assume, we will declare an array of size 10 within the following way.
int A[5];
Here ‘A’ itself may be a pointer which contains the memory location of the primary element of the array. Now for accessing the primary element, we’ll write A[0] which is internally decoded by the compiler as *(A + 0).
In the same way, the second element are often accessed by A[1] or *(A + 1) and so on.
Now let’s assume that array indexing starts at 1 rather than 0. During this case for accessing the primary element, we’ve to write down A[1] which is internally decoded as *(A + 1 – 1).
Observe here that we’ve to perform one extra operation i.e. subtraction by 1. This extra operation will greatly decrease the performance when the program is big. That’s why to avoid this extra operation and improve the performance, array indexing starts at 0 and not at 1.
Different Array Operations
Now that we all know the essential idea behind an array, allow us to now check out the varied operations which will be performed on arrays.
Traverse − It is the operation which prints all the elements present within the array one by one.
Insertion − It adds an element at a position or index of your choice.
Deletion − Deletes the elements present at the mentioned index.
Search − Searches a component within the array using the given index or the even the values.
Update − Updates a component at the given index.
Here’s a read on the various operations in Arrays
Types of Arrays with Examples
The various sorts of arrays are as follows :
- One Dimensional (1D) Array
- Multi-Dimensional (2D and more till ‘n’D ) Array
One-Dimensional Array
A one-dimensional array or 1D array is where the elements are going to be accessible in a sequential order. This sort of arrays are going to be accessible by the subscript of either a column or row index. Let’s see a programming example to get further clarity.
#include<stdio.h>
int main()
{
int i;
int arr[5] = {10,20,30,40,50};
// declaring and Initializing array in C
for (i=0;i<5;i++)
{
// Accessing each variable
printf("Value of arr[%d] is %d \n", i, arr[i]);
}
}
Multi-Dimensional Array
When the dimensions are more than one, then it’s called as a multi-dimensional array. Multidimensional arrays include 2D arrays and 3D arrays till ‘n’D arrays.
Two-Dimensional Arrays
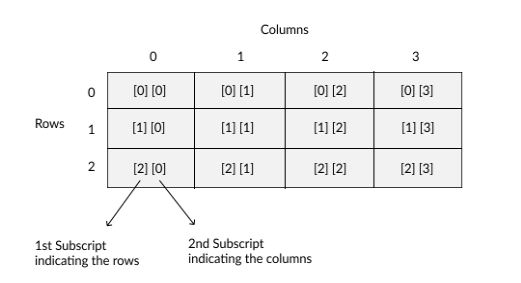
A 2-D Array is generally access by using the subscript of row and column index. For traversing 2-D Array, the worth of the rows and columns is going to be consider. Within the two-dimensional array face [3] [4], the primary index specifies the amount of rows and therefore the second index specifies the amount of columns and the array can hold 12 elements (3 * 4).
Similarly, during a three-dimensional array, there’ll be three dimensions. The array face [5] [8] [10] can hold 400 elements (5 * 10 * 15). Let’s see a programming example to get further clarity.
#include<stdio.h>
int main()
{
int i,j;
// declaring and Initializing array
int arr[2][2] = {10,20,30,40};
for (i=0;i<2;i++)
{
for (j=0;j<2;j++)
{
// Accessing variables
printf("value of arr[%d] [%d] : %d\n",i,j,arr[i][j]);
}
}
}
Three-Dimensional Arrays
A 3-D array is an extension to the 2-D array with addition of depth. In general view, it is a cube that has rows, columns and depth as dimension. To access any element during a 3-D array three subscripts are require for position of element during a specific row, column and depth. The primary index is for depth (dimension or layer), second is for row index and third is for column. Within the example shown the index values (2,0,3) is use to access element 24.
// A sample program for Array Declaration
#include <stdio.h>
int main()
{
int one_dim [5]; # declaration of 1D array
int two_dim [2][2]; #declaration of 2D array
int three_dim [2][3][4] = {
{ {12, 3, 3, 4}, {0, -5, -1, 11}, {23, 22, 33, 2} },
{ {13, 4, 66, 3}, {5, 91, 13, 5}, {3, 11, 24, 89} }
}; #declaration of 3D array. Here the elements are also defined.
return 0;
}
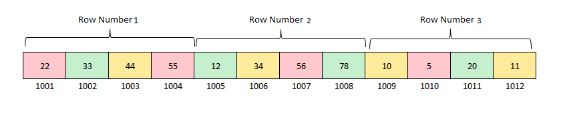
Row Major Representation
In the row major representation the storage of array elements takes place row wise. All elements of first row of the array are first kept in sequence followed by second row then third, fourth then on. The 2-dimensional array given in previous examples is store in row-major representation within the figure below.
Column Major Representation
In the column major representation the storage of array elements takes place column wise. All elements of first column of the array are first kept in sequence followed by second column then third, fourth then on. The 2-dimensional array given in previous examples is store in column-major representation within the figure below.
CONCLUDING — Types of Arrays with Examples
In this post, we saw comprehensively, the different types of arrays with various examples. We also saw the different operations that can be performed on arrays. We also looked into Row Major and Column Major Arrays with the help of quite a lot of great examples. With this, I end this post on a note that you will have understood the topic at hand and take back great knowledge and wisdom. If you have any doubts or need any further inputs and/or clarifications, then feel free to post your queries in the comments section.